Abstract

Why do we have Newton's laws? Is there something deeper underlying principle from which we can acquire Newton's equations of motion? It turns out that all the equations of motion in nature can be obtained by the extremization of certain functional called action S. This action formalism is often introduced to students in the name of principle of least action and in the mathematical form δS=0. The action S, for the entire path, must have an extremum, but not necessarily a minimum. Perhaps the proper name for this formalism may be the principle of stationary action. Now the questions are, If S is extremum (stationary), then what causes it is minimum and for what cases it is maximum? Why in classical mechanics, the action of a correct path is always the minimum? How does the particle find the correct path among infinite incorrect paths? How to go from quantum mechanics back to the classical limit in this action formulation? In this article, I tried to answer these questions in a simple and approachable manner.

Introduction

Let us start with an elementary problem of classical mechanics, say throwing a stone in the air from the ground, and it lands somewhere after some time. Now, the problem is to determine the right trajectory of that stone. Usually, to find the right path, we need to know definite quantities such as the mass of that stone m, a set of forces F involved, and initial conditions. The correct trajectory is the one in which Newton’s laws hold good.

However, we can also formulate the problem of classical mechanics in another way. It is called the principle of least action . This principle is the most general formulation of the law governing the motion of mechanical systems. To understand what this principle is, let us consider a particle in a position x₁ at a time t₁. Let us assume that we know its velocity at that time.

Moreover, we also know that the particle will be at a position x₂ after a given time has elapsed. Now the problem is to find the trajectory taken by the particle. Here is the way to find the true trajectory. The idea is that for each possible trajectory, there is some real number associated with that trajectory called the action S. In classical mechanics, the correct trajectory is the one that minimizes the action S. This principle is called the principle of least action. In general, the action S for the entire true trajectory must have an extremum, but not necessarily a minimum. In the following sections, we will understand why in classical mechanics, we consider only the minimum action principle?

The principle of extreme action is the most compact form of laws of nature. It summarizes everything, not only classical mechanics but electrodynamics, relativities, quantum mechanics, and particle physics.

The action S in Quantum mechanics

To answer the question mentioned above, we need to invoke a quantum mechanical perspective. So, let us relate the action to quantum mechanics. In quantum mechanics, we have complex wave functions, so a plane wave looks like this Ψ = Ae^{i(kx − ωt)} = Ae^iΦ. The phase is, Φ = kx − ωt, From de-Broglie’s relation $P = \frac{h}{\lambda}$ and the Einstein’s equation E = hf = H, we have, $$\Phi=\frac{1}{\hbar}(Px-H t).$$ Nevertheless, this is only true for a plane wave, in which the wave number and momentum are constant, and the frequency and the energy are constant. If the wave number is changing, the wavelength is changing then, for each part of the motion the increment of the phase is $$\Delta\Phi=\frac{1}{\hbar}(P\Delta x-H\Delta t),$$ pull out a factor of Δt, $$\Delta\Phi=\frac{1}{\hbar}(Pv-H)\Delta t,$$ now recognize the bracket as the lagrangian, $$\Delta\Phi=\frac{1}{\hbar}{\cal L}\Delta t,$$ $$\Phi=\frac{1}{\hbar}\int\limits_{}^{}{\cal L}\Delta t = \frac{S}{\hbar},$$ So, the non-relativistic quantum mechanical wave function in terms of the action S is given by $$\Psi=A~e^{i\frac{S}{\hbar}}.$$ This is an important result: The quantum mechanical phase is just S/ℏ.

Is the Action minimum or maximum?

Now, we are ready to tackle our questions. Let us start from a classical particle that moves from position x₁ to position x₂ in a given amount of time t.

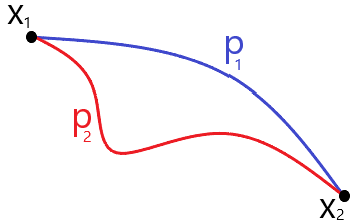
Let us consider two different paths. The path p₁ is a classically correct path with a minimum action, and path p₂ is a classically incorrect path that does not satisfy Newton’s laws of motion. However, How does the particle find the right path? In Newtonian mechanics, a particle’s current position results from all the forces that acted on it in the past. Every moment it gets an acceleration. However, the principle of least action appears to reframe the physics by saying that "If the particle ends up in some position, then it might take a precise path, namely the one that minimizes the action." Is it mean that the particle already knows where it will finally be?

Let us try to understand our problem from the quantum mechanical perspective. In the quantum description, the probability amplitude for these two paths have different phases S/ℏ. (because both have different action S), but the same magnitudes. So the probability (square of the probability amplitude) of going along either path is the same. The correct path and any incorrect path are in some sense equally probable. That is weird. Nevertheless, suppose we are looking at a classical system. In that case, that means we are not looking at it in fine resolution. So, It is an excellent approximation to consider our classically correct paths as a bunch of paths around the path p₁ and incorrect path as another bunch of paths around the path p₂. Here, a bunch, in a sense, these paths are surrounded by several nearby paths.

Now, consider a bunch of paths built around the path p₁. Its neighboring paths within that bunch would have a different action S because the action changes when there is a small shift of the path. The phase is S/ℏ. Thus, even if S differs slightly but because of ℏ in the denominator, the phase differs significantly. Therefore, if we look at a bunch of paths around a classically incorrect path, all the neighboring paths have totally different phases. When we add them all up, the result is basically zero (destructive interference).

However, For the correct classical path p₁. Its neighboring path within that bunch would have almost the same action S because action S of the path p₁ is minimum. So, the path p₁ and all its neighboring paths within that bunch all give the same phase in the first approximation. When we add them up, we will get a large overall amplitude (constructive interference) .

In the actual quantum scenario, there are infinite possible paths. The probability that a particle is traveling from a position x₁ and arrives at a position x₂ in a given amount of time t is the square of the sum of the amplitudes of each possible path. When we add all the amplitudes, all the paths with the action S vary in the first approximation will basically disappear (destructive interference). The path with minimum action S and its neighboring paths for which the action S does not vary in the first approximation are the only bunch of paths that stand out because of constructive interference. This is the reason why classical motion seems to pick out the path of minimum action S. (This is analogous to how the light chooses the shortest time taken path.

The principle of extreme action is incompletely stated in classical mechanics; the proper statement is (maybe) particle follows all infinite possible paths (that even include paths going backward in time) and total probability amplitudes of each path added up to zero except the paths with the action S does not vary in the first approximation. It turns out in classical mechanics that the path is the one that minimizes the action S.

The passage from the action formulation to quantum mechanics was carried out by the physicist Richard Feynman in his Ph.D. thesis titled “The Principle of Least Action in Quantum Mechanics" in 1942.

Conclusion

So, In the quantum scale, a particle follows all infinite possible paths. In other words, the notion of trajectory is meaningless in the quantum scale, so quantum particle has no precise position and momentum simultaneously. The principle of stationary action is the reason why we have the Heisenberg uncertainty principle (indeterminacy principle) in quantum mechanics.

I hope I have briefly explained why classical motion seems to pick out the path of minimum action S. This paper is targeted toward advanced undergraduate and master students who are trying to understand the action principle for the first time. For further readings, kindly refer to the bibliography section.

Acknowledgments

I like to thank my mentor Dr. Harleen Dahiya, Dr. Abhinav Pratap Singh and my friend Mr. Rajesh Kumar who helped me clarify numerous points in this manuscript and encour- aged the interest that made this writing possible. I also thank Ms. Sarabjot Kaur for her valuable feedback and motivation.

Appendix: How does the light choose the shortest time taken path?

If the light went on a path that took a different amount of time, it would arrive at a different phase. Moreover, the total amplitude at some point is the sum of contributions of amplitude for all the different ways the light can arrive. All the paths that give wildly different phases do not add up to anything. However, suppose we can find a whole sequence of paths that have phases almost all the same. In that case, the little contributions will add up, and we get a reasonable total amplitude to arrive. The important path becomes the one for which there are many nearby paths that give the same phase .

References

Prof.V.Balakrishnan (IIT-M), The NPTEL Lecture series on Classical Physics, (2009).

Prof. Leonard Susskind, The Theoretical Minimum course on Classical Mechanics course, (2011).

Prof. Kenneth Young, A Special Lecture on the Principle of Least Action, (2014).

Prof. Thanu Padmanabhan (IUCAA), A Special Lecture on The Action in Physics, (2017).

Prof.Leonard Susskind, Theoretical Minimum course on Particle Physics 1: Basic Concepts, (2010).

R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Addison-Wesley (Reading, Mass., USA), Vol. II, Chapter 19, (1963).

Prof.Richard Feynman, Feynman’s Thesis: A New Approach to Quantum Theory, World Scientific (2005).

R. P. Feynman, R. B. Leighton, and M. Sands, The Feynman Lectures on Physics, Addison-Wesley (Reading, Mass., USA), Vol. I, Chapter 26, (1963)